评析   成都市青羊区教科院   潘绍茂　　

                                                                      授课   成都市青羊实验中学   何  磊　　

【案例描述】　　

2017年11月6--7日，全国差异教学研讨会在成都青羊召开，成都市青羊实验中学何磊老师一节“反比例函数K的几何意义”一课受到与会者好评，得到差异教学创始人华国栋教授肯定。　　

一、教学设计　　

1.教学基础目标：　　

（1）了解反比例函数中“k”的值与相应矩形及三角形面积之间的关系。　　

（2）通过不断地变化，掌握能在不同的图形中应用基本图形来解决问题。　　

（3）能在题目不同的变化中发现题目的共性，并能自己归纳总结适合自己的思考经验和解题技巧。　　

2.教学差异目标：　　

（1）对上节课的认识还比较模糊地学生，要求通过本节课的学习加强对上一节课知识的认识，并对本节课的知识有初步了解，要能知道“k”值求所得矩形和三角形的面积。　　

（2）对上节课掌握了基本知识并能简单应用的学生，要求通过本节课的探究学习合作交流，巩固上节知识，熟练应用本节新知解决实际问题。理解“k”对矩形和三角形面积的影响，要能知“k”求面积，也要能知面积求“k”，并能在一般变化中熟练应用。　　

（3）对于上节知识掌握很好并能灵活应用的学生，在熟知本节知识点的前提下，理解“k”几何意义的内涵，在复杂的图形变化中探索解决问题一般方法，并能进行归纳和提炼，还要能对本节知识进行拓展与延伸，为后继学习打下基础。　　

二、协作学习环境设计　　

课前测问题发布在“猿题库”里，学生先学习，课件，微视频、学案（上课前一天发在qq群，让学生先观看）　　

三、教学重、难点　　

重点：通过观察图象，概括反比例函数图象的共同特征，探索反比例函数的比例系数“k”的几何意义，理解过双曲线上任意一点向x轴y轴作垂线所得矩形面积等于k的绝对值，过双曲线上任意一点向x轴或y轴作垂线并连接该点与坐标原点所得三角形面积等于k的绝对值的一半，并能够在不同变化中熟练使用。努力完成不同的挑战性目标。　　

难点：从反比例函数的图象中归纳总结反比例函数的主要性质及综合应用。　　

四、教学过程（片段）　　

（一）预学查异：课前测了解学生的差异　　

（1）反比例函数　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　上一点A（4，3）　　

问题  ①该反比例函数的解析式是什么？　　

②矩形ABOC的面积是多少？△AOB的面积又是多少呢？　　

（2）反比例函数　 　　　上一点A（-4，3）　　

问题①该反比例函数的解析式是什么？　　

②矩形ABOC的面积是多少？△AOB的面积又是多少呢？　　

【这是老师在课前测时学生错误较多的问题，老师通过学生讲解思路，了解错误原因，让学生自主改正或者同学帮助解决。】　　

师：完成了的同学请思考：矩形ABOC的面积和△AOB的面积与反比例函数比例系数有什么联系？　　

【老师的提问，为本节课的学生作了很好的铺垫，待学生回答正确后，老师提出下列问题】　　

（二）研学导异：当基础目标达成后，出示具有挑战性的教学内容　　

问题：　　

师：矩形OAPB和△OAP面积会随着P点位置的变化而变化吗？　　

思考：反比例函数比例系数k的几何意义是什么？　　

【学生六个人一组讨论，教师有时间下位到学生中间，指导学习有困难的学生，教师心中有“隐性的学生层次”，结束后教师每一个组提问一个学生代表，其他学生不错，这个环节学生发言踊跃。学生是否掌握，通过出示问题2，看学生的反馈情况。】　　

2.反比例函数　 　　　的图象如图所示，点A是该函数图象上任意一点，AB⊥x轴于点B，如果S△AOB＝2，请求k的值。　　

【本问题时前面问题的逆向思考，已知面积求K，难度不大，学生能计算准确。】　　

（三）拓学展异：分层与同质分组相结合，大面积反馈与多元评价相结合　　

例：如图，矩形ABCD的边分别平行于坐标轴且对角线BD经过坐标原点O，若点A的坐标为（﹣2，﹣3），OE:OG=1:3，试分别求过点A、点B、点C、点D的反比例函数图象的解析式。

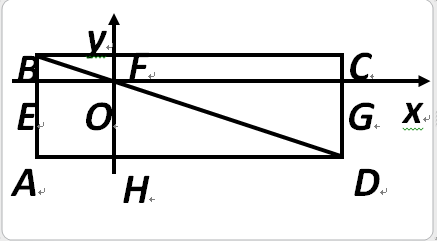
【本题的解决是本节课的高潮，求过点A、点B、点C、点D的反比例函数图象的解析式，难度不同，方法各异，教师这时用学生喜闻乐见的扑克牌花色代表不同难度进行分组，共分成核桃、红桃、樱花和方块4组，核桃组求过D点的解析式、红桃组求过C点的解析式、樱花组求过B点的解析式，方块组求过A点的解析式，学生自主选择，完成后全班交流，这时学生学习积极性高涨，讨论热烈，对于求过点C、D的解析式，主要是求点的坐标，学生用到不同的方法，有用几何方法相似求点的坐标，有用代数方法求点的坐标，学生的思维得到了最大的发展。】　　

【案例分析】　　

课堂教学中开展差异教学，我们通过学习《差异教学策略》，基于三个相信开展，即相信一个班的学生存在差异；相信针对学生的差异开展教学有效果；相信学生在多种教学方法教学下能得到最大的发展。差异教学可以发挥教师和学生的双主体性，以学生的个体发展为目标，让学生在参与中获取知识，让不同水平的学生都有同等的参与和发展机会。根据学生不同的学习类型、认知风格、准备状态差异设计不同层次的数学问题，让学生选择自己胜任的学习任务来主动参与学习，使“教与学”得到最大限度的匹配，正是我们数学教学中要“求”的教学效果最大值。